Research topics
|
|
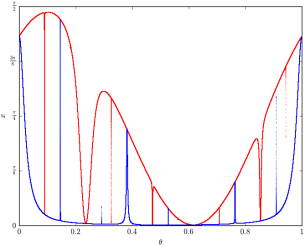
Quasiperiodically forced systems Quasiperiodic forcing is the simplest type of aperiodic driving that can occur in dynamical systems. In the modelling of real-world phenomena, it comes up whenever the process in question is influenced by two or more periodic external factors with incommensurate frequencies. Examples are multi-frequency forced oscillators or electric circuits and Schrödinger operators with quasiperiodic potential. One phenomenon which has attracted particular interest in qpf systems is the wide-spread occurrence of so-called strange non-chaotic attractors (SNA). These objects combine a complicated structure with non-chaotic dynamics, a combination which is quite rare in dynamical systems otherwise. Another interesting aspect of qpf 1D-maps is that they can be considered either as 1D non-autonomous systems or as autonomous 2D-maps with a special skew product structure. In both situations, they can serve as simple models whose study allows to obtain further insights about the general case. |
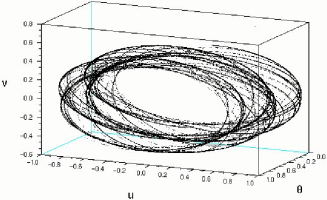 |
Non-autonomous bifurcation theory One of the primary goals of non-autonomous bifurcation theory is the description of non-autonomous counterparts of the classical bifurcation pattern of dynamical systems. The external forcing often leads to qualitative changes of the bifurcation scenario. For example, saddle-node bifurcations may become non-smooth (thus involving strange non-chaotic attractors) and the usual Hopf bifurcation pattern gives way to the two-step scenario for the non-autonomous Hopf bifurcation proposed by Ludwig Arnold. |
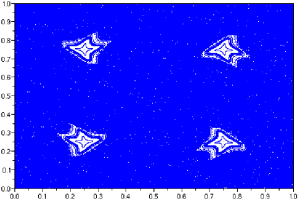 |
Dynamics of surface homeomorphisms Rotation theory is one of the main tools to understand and classify the dynamical behaviour on surfaces. Originated by Henri Poincare in the context of orientation-preserving circle homeomorphisms and flows on the two-torus, it has further been developed for twist maps of the annulus and homeomorphisms of the torus. However, many fundamental questions still remain open, in particular for the case of torus homeomorphisms. |